MVP Matrix

MVP 矩阵即 Model（模型）、View（观察）、Projection（投影）矩阵。

Model

模型矩阵描述的是 3D Point 的仿射变换，包含 Scale（缩放）、Rotate（旋转）、Translate（平移）。

可以按照下面的方式表示： \[ M = Scale \times Rotate \times Translate \]

  • 最后进行 Translation 是为了保证前面的操作参考坐标轴不会变化。
  • OpenGL 是左乘的，因此编程时计算模型矩阵需要按照 Translate、Rotate、Scale 的顺序进行。

写的具体一点如下： \[ \begin{bmatrix} \hat{x}\\ \hat{y}\\ \hat{z}\\ 0\\ \end{bmatrix}= \begin{bmatrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{bmatrix}\times \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} \] 之所以用 4 × 4 的矩阵来表示，是为了统一用矩阵乘法。如果用 3 × 3 的矩阵，会导致计算 Translate 变化时，只能用 3 × 3 的矩阵矩阵加法来表示。并且这样可以用来区分点（Point）和向量（Vector）。

  • 3D Point \([x,y,z,1]^T\) (w = 1，Translate OK)
  • 3D Vector \([x,y,z,0]^T\)(w = 0，No Translate)
  • 3D Point + 3D Point（w = 2，Middle Point）
  • 3D Point - 3D Point （w = 0，3D Vector）
  • 3D Point + 3D Vector（w = 0，3D Point）
  • 3D Vector + 3D Vector（w = 0，3D Vector）

define \([x,y,z,w]^T(w \neq 0)\) is the 3D Point \([x/w,y/w,z/w,1]^T\) 。

这种定义叫做齐次坐标（Homogeneous coordinates）。

View

观察矩阵用于将模型投影到摄像机（Camera）上。

一般而言，定义观察矩阵（或者说摄像机状态）需要下面的一些参数：

  • Position：摄像机位置 \(P = [x_p,y_p,z_p]^T\)
  • Up：摄像机上方 \(U = [x_u,y_u,z_u]^T\)
  • LookAt：摄像机观察方向 \(L = [x_l,y_l,z_l]^T\)
  • Right：摄像机右方 \(R = L \times U = [x_r, y_r, z_r]^T\)

为了推导出实际的 View 矩阵（记为 \(V\)），假设初始状态如下的 View 矩阵（记为 \(V_0\)）的参数如下：

  • \(P = [0,0,0]^T\)（原点）
  • \(U = [0,1,0]^T\)（正 Y 轴）
  • \(L = [0,0,-1]^T\)（负 Z 轴）
  • \(R = [1,0,0]\)（正 Z 轴）

注意，对于观察者而言，我们要感受到物体进行了平移旋转之类的操作，需要对 View 矩阵（摄像机）进行相反的操作。要得到实际 View 矩阵，需要进行逆变换\(V \rightarrow V_0\)，其操作具体如下：

  • Translate
    • P：\([x_p,y_p,z_p]^T \rightarrow [0,0,0]^T\)
  • Rotate：
    • U：\([x_u,y_u,z_u]^T \rightarrow [0,1,0]^T\)
    • L：\([x_l,y_l,z_l]^T \rightarrow [0,0,-1]^T\)
    • R：\([x_l,y_l,z_l]^T \times [x_u,y_u,z_u]^T = [x_r, y_r, z_r]^T \rightarrow [1,0,0]^T\)

对于 Translate，容易得到 \[ V_T= \begin{bmatrix} 1 & 0 & 0 & -x_p\\ 0 & 1 & 0 & -y_p\\ 0 & 0 & 1 & -z_p\\ 0 & 0 & 0 & 1 \end{bmatrix} \] 对于 Rotate，不方便直接计算，考虑逆向情况：

  • R：\([x_l,y_l,z_l]^T \times [x_u,y_u,z_u]^T = [x_r, y_r, z_r]^T \rightarrow [1,0,0]^T\)（X 轴方向）
  • U：\([x_u,y_u,z_u]^T \rightarrow [0,1,0]^T\)（Y 轴方向）
  • L：\([-x_l,-y_l,-z_l]^T \rightarrow [0,0,1]^T\) （Z 轴方向）

因此有： \[ V_R^{-1}= \begin{bmatrix} x_r & x_u & -x_l & 0\\ y_r & y_u & -y_l & 0\\ z_r & z_u & -z_l & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \] 注意到旋转矩阵在实际中会使用正交矩阵，即： \[ V_R = (V_R^{-1})^{-1} = (V_R^{-1})^{T}= \begin{bmatrix} x_r & y_r & z_r & 0\\ x_u & y_u & z_u & 0\\ -x_l & -y_l & -z_l & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \] 因此实际的 View 矩阵为： \[ V = V_R \times V_T = \begin{bmatrix} 1 & 0 & 0 & -x_p\\ 0 & 1 & 0 & -y_p\\ 0 & 0 & 1 & -z_p\\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x_r & y_r & z_r & 0\\ x_u & y_u & z_u & 0\\ -x_l & -y_l & -z_l & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

Projection

Projection （投影）矩阵一般分为 Orthographic Projection（正视投影）和 Perspective Projection （透视投影）。

Orthographic Projection

之前在 Games101 上看到闫令琪老师的定义感觉很清晰：

Map a cuboid \([l,r] \times [b, t] \times [f, n]\) to the canonical cube \([-1, 1]^3\)。

  • 这里的是右手系，所以远平面 f 在前面（比如 OpenGL 中的前面一般认为是负 Z 轴，f < n）;

要完成正视投影，只需要两步即可：

  • Translate \(Centor Point \rightarrow [0,0,0]^T\)
  • Scale \([2,2,2]^T\)

可以很容易得到正视投影矩阵为： \[ P = P_O = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix} \] Perspective Projection

透视投影可以通过挤压远平面 f 来变成正交投影。

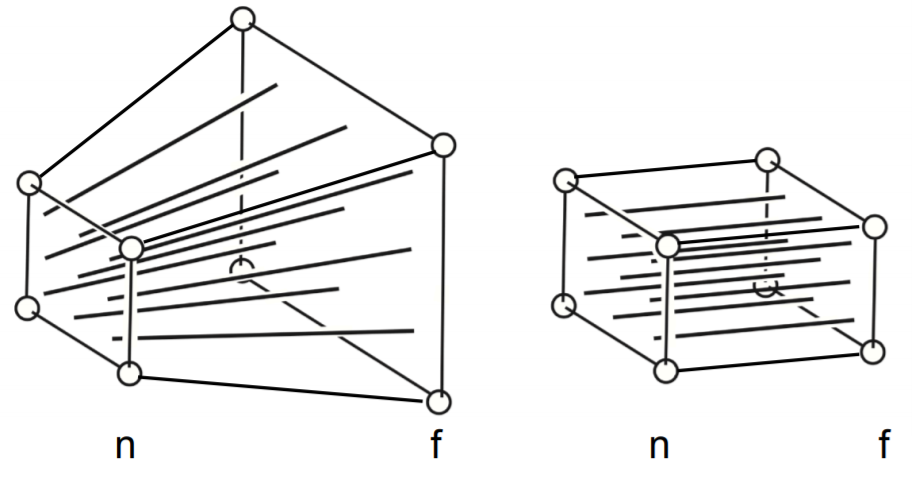
并且有下面的规定：

  • 近平面 n 上的点经过挤压后坐标不变。
  • 远平面 f 上的中心点挤压后坐标不变。
  • 远平面 f 上的点经过挤压后 z 坐标不变（z = f）。

对于某一点 \([x,y,z]^T\)，经过变换后变为 \([x',y',z']^T\)。

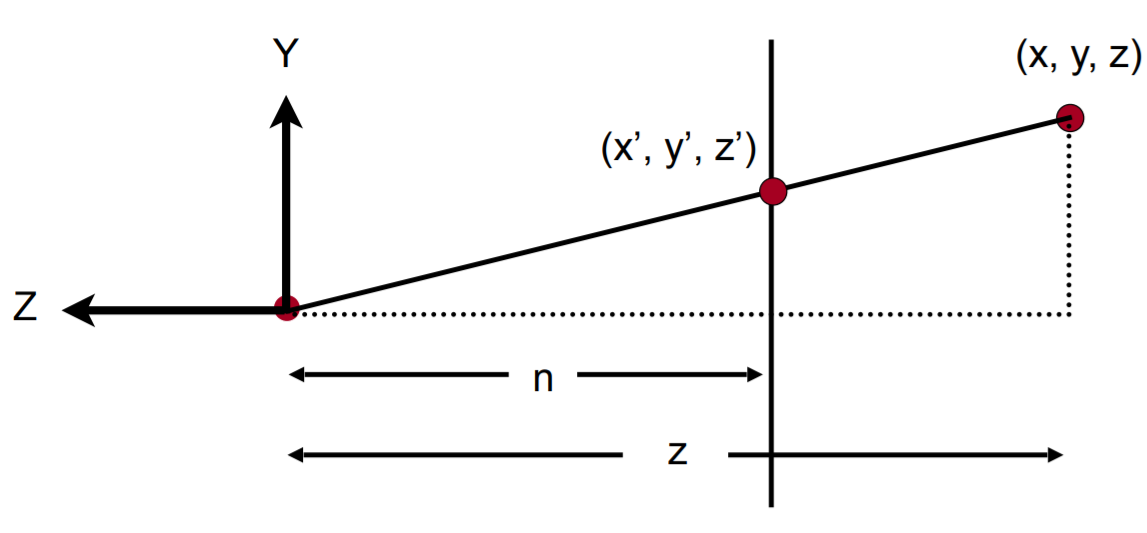
明显有： \[ y'= \frac{n}{z}y \] 类似有： \[ x'= \frac{n}{z}x \] 在齐次坐标中，可以写出下面的式子（3D Point，w = 1）： \[ \begin{bmatrix} x\\ y\\ z\\ 1\\ \end{bmatrix} \longrightarrow \begin{bmatrix} \frac{n}{z}x\\ \frac{n}{z}y\\ ?\\ 1\\ \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ ?\\ z\\ \end{bmatrix} \] 记矩阵 \(P_{P\rightarrow O}\) 表示从透视矩阵转为正交矩阵的矩阵： \[ P_{P \rightarrow O} \times \begin{bmatrix} x\\ y\\ z\\ 1\\ \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ ?\\ z\\ \end{bmatrix} \] 由于： \[ P_{P \rightarrow O}[1] \cdot \begin{bmatrix} x\\ y\\ z\\ 1\\ \end{bmatrix} = nx \] 即： \[ P_{P \rightarrow O}[1] = [n, 0, 0, 0] \] 同理： \[ P_{P \rightarrow O}[2] = [0, n, 0, 0] \]

\[ P_{P \rightarrow O}[4] = [0, 0, 1, 0] \]

由于任何近平面 n 上的点坐标不变，因此： \[ \begin{bmatrix} x\\ y\\ n\\ 1\\ \end{bmatrix} \longrightarrow \begin{bmatrix} x\\ y\\ n\\ 1\\ \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ n^2\\ n\\ \end{bmatrix} \] 即： \[ P_{P \rightarrow O}[3] \cdot \begin{bmatrix} x\\ y\\ n\\ 1\\ \end{bmatrix} = n^2 \] 由于和 \(n^2\) 与 \(x、y\) 无关，因此前两项必为 0： \[ [0, 0, a, b] \cdot \begin{bmatrix} x\\ y\\ n\\ 1\\ \end{bmatrix} = n^2 \] 化简有： \[ an + b = n^2 \] 由于任何远平面 f 上的中心点 \([0,0,f]^T\) 坐标不变，因此： \[ \begin{bmatrix} 0\\ 0\\ f\\ 1\\ \end{bmatrix} \longrightarrow \begin{bmatrix} 0\\ 0\\ f\\ 1\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ f^2\\ f\\ \end{bmatrix} \] 即： \[ [0, 0, a, b] \cdot \begin{bmatrix} 0\\ 0\\ f\\ 1\\ \end{bmatrix} = f^2 \] 化简有： \[ af + b = f^2 \] 联立解得： \[ \left\{\begin{matrix} a = n + f\\ b = -nf \end{matrix}\right. \] 因此： \[ P_{P \rightarrow O} = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n + f & -nf\\ 0 & 0 & 1 & 0 \end{bmatrix} \] 最终计算出透视投影矩阵为： \[ P_P = P_O \times P_{P \rightarrow O} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n + f & -nf\\ 0 & 0 & 1 & 0 \end{bmatrix} \]