Quaternion and Rotation
Quaternion
define: \[ q = a + b\textbf{i} + c\textbf{j} + d\textbf{k}, ~~\textbf{i}^2 =\textbf{j}^2 = \textbf{k}^2 = \textbf{i}\textbf{j}\textbf{k} = -1 \] \(\textbf{i},\textbf{j},\textbf{k}\) are perpendicular to each other: \[ \textbf{i} \perp \textbf{j} \perp \textbf{k} \] a is perpendicular the 3D space \(\textbf{i}-\textbf{j}-\textbf{k}\): \[ a\perp \textbf{i},~~a\perp \textbf{j},~~a\perp \textbf{k} \] let: \[ \vec{v} = b\textbf{i} + c\textbf{j} + d\textbf{k} \] so: \[ q = a + \vec{v} \] define: \[ unit~~quaternion = \frac{q}{||q||} \]
\[ q q^{-1} = q^{-1} q = 1(unit~~quaternions) \] so: \[ q^{-1} = (a + \vec{v})^{-1} = \frac{(a + \vec{v})^*}{||a+\vec{v}||^2} = \frac{a - \vec{v}}{a^2+||\vec{v}||^2} \]
for each \(q_1 = a_1 + \vec{v_1},q_2 = a_2 + \vec{v_2}\)
addition: \[ q_1 + q_2 = (a_1 + a_2) + (\vec{v_1} + \vec{v_2}) \] multiplication: \[ q_1 q_2 = (a_1 a_2 - \vec{v_1} \cdot \vec{v_2}) + (a_1 \vec{v_2} + a_2 \vec{v_1} + \vec{v_1} \times \vec{v_2}) \]
Rotation
A rotation of \(\theta\) around the axis \(\vec{u}\): \[ \vec{u} = (u_x, u_y, u_z) = u_x\textbf{i} + u_y\textbf{j} + u_z\textbf{k} \] It can be represented by a quaternion \(q\) ,an extension of Euler's formula: \[ q = e^{\frac{\theta}{2}(u_x\textbf{i} + u_y\textbf{j} + u_z\textbf{k})} = cos(\frac{\theta}{2}) + (u_x\textbf{i} + u_y\textbf{j} + u_z\textbf{k}) sin(\frac{\theta}{2}) \] Given \(p\) in 3D space,and the real part is zero : \[ \vec{u} = (u_x, u_y, u_z) = 0 + u_x\textbf{i} + u_y\textbf{j} + u_z\textbf{k} \] We can get \(\hat{p}\): \[ \hat{p} = q p q^{-1} \] there: \[ q^{-1} = e^{-\frac{\theta}{2}(u_x\textbf{i} + u_y\textbf{j} + u_z\textbf{k})} = cos(\frac{\theta}{2}) - (u_x\textbf{i} + u_y\textbf{j} + u_z\textbf{k}) sin(\frac{\theta}{2}) \]
You can find proof below.
Example
Define the rotation function \(f_r\) around the axis \(\vec{v} = \textbf{i} + \textbf{j} + \textbf{k}\),and the \(\theta = 120^{\circ}\).
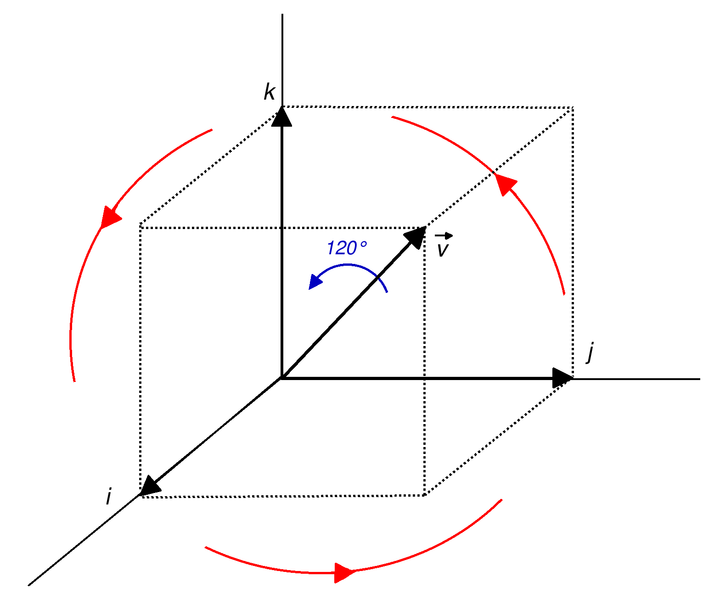
Calculate \(q\):(normalize \(\vec{v}\)) \[ q = cos(\frac{\theta}{2}) + \frac{\vec{v}}{||\vec{v}||}sin(\frac{\theta}{2}) = \frac{1 + \textbf{i} + \textbf{j} + \textbf{k}}{2} \] So the \(f_r\) is: \[ f_r(a\textbf{i} + b\textbf{j} + c\textbf{k})=q(a\textbf{i}+b\textbf{j}+c\textbf{k})q^{-1} \] there: \[ q^{-1} = \frac{1 - \textbf{i} - \textbf{j} - \textbf{k}}{2} \] So the actual \(f_r\) is: \[ f_r(a\textbf{i} + b\textbf{j} + c\textbf{k}) = \frac{1 + \textbf{i} + \textbf{j} + \textbf{k}}{2} (a\textbf{i} + b\textbf{j} + c\textbf{k}) \frac{1 - \textbf{i} - \textbf{j} - \textbf{k}}{2} \]
Rotation Proof
Let \(\vec{p}\) around the rotation axis \(\vec{A}\) ratate \(\theta\),there: \[ ||\vec{A}|| = 1 \] So the projection of \(\vec{p}\) on \(A\) is: \[ p_{A} = cos<\vec{p},\vec{A}> ||\vec{p}|| \vec{A} = \frac{\vec{A} \cdot \vec{p}}{||\vec{p}||}||\vec{p}|| \vec{A} = \vec{A} \vec{p} \vec{A} \] The vertical direction vector is: \[ p_{\perp A} = \vec{p} - \vec{A} \vec{p} \vec{A} \] After rotation,\(p_{A}\) don't change.
We can get \(\hat{p}\) by the linear combination of \(p_{\perp A}\) and \(\vec{A} \times \vec{p}\).
\(p_{\perp A}\) rotate around the axis \(A\) with the degree of \(\theta\). \[ p_{\perp A}' = p_{\perp A} cos(\theta) + (\vec{A} \times \vec{p}) sin(\theta) \] So the \(\vec{p}'\) is: \[ \vec{p}' = p_{A} + p_{\perp A}' = \vec{A} \vec{p} \vec{A} +(\vec{p} - \vec{A} \vec{p} \vec{A})cos(\theta) + (\vec{A} \times \vec{p})sin(\theta) \]
\[ \vec{p}' = \vec{p}cos(\theta) + (\vec{A} \times \vec{p})sin(\theta) + (\vec{A} \vec{p} \vec{A})(1 - cos(\theta)) \]
For Euler Angels,it is easy to get: \[ R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \end{bmatrix} \]
\[ R_y(\beta) = \begin{bmatrix} cos(\beta) & 0 & sin(\beta) \\ 0 & 1 & 0\\ -sin(\beta) & 0 & cos(\beta) \end{bmatrix} \]
\[ R_z(\gamma) = \begin{bmatrix} cos(\gamma) & -sin(\gamma) & 0 \\ sin(\gamma) & cos(\gamma) & 0\\ 0 & 0 & 0 \end{bmatrix} \]
\[ R_{xyz} = R_x(\alpha)R_y(\beta)R_z(\gamma)\\ = \begin{bmatrix} cos(\beta)cos(\gamma) & cos(\beta)sin(\gamma) & -sin(\theta)\\ sin(\alpha)sin(\beta)cos(\gamma) - cos(\alpha)cos(\gamma) & sin(\alpha)sin(\beta)sin(\gamma) + cos(\alpha)cos(\gamma) & sin(\alpha)cos(\beta)\\ cos(\alpha)sin(\beta)cos(\gamma) + sin(\alpha)sin(\gamma) & cos(\alpha)sin(\beta)sin(\gamma) - sin(\alpha)cos(\gamma) & cos(\alpha)cos(\beta)\\ \end{bmatrix} \]
Gimbal Lock
when \(\beta\) = 0: \[ R_{xyz}= \begin{bmatrix} 0 & 0 & -1 \\ sin(\alpha - \gamma) & cos(\alpha - \gamma) & 0\\ cos(\alpha - \gamma) & -sin(\alpha - \gamma) & 0 \end{bmatrix} \] Lost freedom in one direction.
Quaternion Rotation Proof
Let \(q = a + \vec{v}\) is a unit quaternion,so: \[ q^{-1} = \frac{a - \vec{v}}{||q||} = a - \vec{v} \] We can prove : \[ \hat{p} = q p q^{-1} = (a + \vec{v}) p (a - \vec{v}) = (a + \vec{v})(0 + \vec{p}) (a - \vec{v})\\ =(-\vec{v} \cdot \vec{p} + a\vec{p} + \vec{v} \times \vec{p})(a - \vec{v}) \\ =a^2\vec{p} + 2a(\vec{v} \times \vec{p}) + (\vec{v} \cdot \vec{p})\vec{v} - \vec{v} \times \vec{p} \times \vec{v} \] Because \(\vec{v} \times \vec{p}\) is perpendicular to \(\vec{v}\) : \[ \vec{v} \times \vec{p} \cdot \vec{v} = 0 \] and: \[ -a (\vec{p} \times \vec{v}) = a(\vec{v} \times \vec{p}) \]
Theory:For each \(\vec{p},\vec{q} \in R^3\): \[ \vec{p} \times \vec{q} \times \vec{p} = \vec{p} \times (\vec{q} \times \vec{p}) = \vec{p}^2\vec{q} - (\vec{p} \cdot \vec{q})p \]
By this theory: \[ - \vec{v} \times \vec{p} \times \vec{v} = (\vec{v} \cdot \vec{p})v - \vec{v}^2\vec{p} \] so: \[ \hat{p} = (a^2 - \vec{v}^2)p + 2a(\vec{v} \times \vec{p}) + 2(\vec{v} \times \vec{p})\vec{v} \] Let \(\vec{v} = t \vec{e},~~||\vec{e}|| = 1\),then: \[ \hat{p} = (a^2 - t^2)\vec{p} + 2at(\vec{e} \times \vec{p}) + 2t^2(\vec{e} \cdot \vec{p})\vec{e} \] compare with: \[ \vec{p}' = \vec{p}cos(\theta) + (\vec{A} \times \vec{p})sin(\theta) + (\vec{A} \vec{p} \vec{A})(1 - cos(\theta)) \] We can get: \[ \left\{\begin{matrix} a^2 - t^2 = cos(\theta)\\ 2at = sin(\theta)\\ 2t^2 = 1 - cos(\theta) \end{matrix}\right. \] Solve the equation group: \[ \left\{\begin{matrix} t = \sqrt{\frac{1 - cos(\theta)}{2}} = sin(\frac{\theta}{2})\\ a = cos(\frac{\theta}{2}) \end{matrix}\right. \] so: \[ q = a+\vec{v} = cos(\frac{\theta}{2}) + \frac{\vec{v}}{||\vec{v}||}sin(\frac{\theta}{2}) \] We can use \(q_1 q_2 \cdots q_n\) represent a series of rotation.
Quaternion Rotation Matrix
The rotation \(\hat{p} = q p q^{-1}, q = a + t\vec{e}\) can be represented by a matrix \(\hat{p} = Rp\): \[ qpq^-1 = (\begin{bmatrix} a^2 - t^2 & 0 & 0 \\ 0 & a^2 - t^2 & 0 \\ 0 & 0 & a^2 - t^2 \\ \end{bmatrix}+ \begin{bmatrix} 0 & -2at\vec{e}_z & 2at\vec{e}_y \\ 2at\vec{e}_z & 0 & -2at\vec{e}_x \\ -2at\vec{e}_y & 2at\vec{e}_x & 0 \\ \end{bmatrix}+ \begin{bmatrix} 2t^2\vec{e}_x^2 & 2t^2\vec{e}_x\vec{e}_y & 2t^2\vec{e}_x\vec{e}_z \\ 2t^2\vec{e}_x\vec{e}_y & 2t^2\vec{e}_y^2 & 2t^2\vec{e}_y\vec{e}_z \\ 2t^2\vec{e}_x\vec{e}_y & 2t^2\vec{e}_y\vec{e}_z & 2t^2\vec{e}_z^2 \\ \end{bmatrix})p \] let : \[ q = (w, x, y, z) \] so: \[ \left\{\begin{matrix} w = a\\ x = t\vec{e}_x\\ y = t\vec{e}_y\\ z = t\vec{e}_z\\\end{matrix}\right. \] then: \[ x^2 + y^2 + z^2 = t^2 \vec{e}^2 = t^2 \] Bring in and simplify: \[ R = \begin{bmatrix} 1 - 2y^2 - 2z^2 & 2xy - 2wz & 2xz + 2wy \\ 2xy + 2wz & 1 - 2x^2 - 2z^2 & 2yz - 2wx \\ 2xz - 2wy & 2yz + 2wx & 1 - 2x^2 - 2y^2 \end{bmatrix} \]
- 本文链接:https://morisa66.github.io/2021/02/10/Quaternion/
- 版权声明:本博客所有文章除特别声明外,均默认采用 许可协议。

