判断两个四边形是否相交

如果是矩形，这个问题很简单，但这里是一般的凸多边形。

我的思路是利用矩阵叉乘判断是存在某个四边形的顶点在另一个四边形的里面来判断是否相交的。

在边上的情况我定义为相交，如下图：

很容易证明：当两个四边形相交时，其中一个四边形必然至少有一个顶点在另一个四边形的内部。

对于凸多边形\(A:A_1A_2\cdots A_n\)和点\(P\)，若\(P\)在多边形每一条边\(A_1A_2\cdots A_nA_1\)的同一边，即下面的表达式同号，则可以证明\(P\)在\(A\)的内部。 \[ \vec{A_1A_2} \times \vec{A_1P} \\ \vec{A_2A_3} \times \vec{A_2P} \\ ... \\ \vec{A_nA_1} \times \vec{A_nP} \] 算法实现：

  • 对于四边形A的每个顶点，判断其是否在四边形B里面（或边上），如果判断在里面，则直接返回在AB相交。
  • 对于四边形B的每个顶点，判断其是否在四边形A里面（或边上），如果判断在里面，则直接返回在AB相交。
  • 没有在里面（或边上）的顶点，返回AB不相交。

对于任意的凸多边形，都可以按照这样的算法来判断。

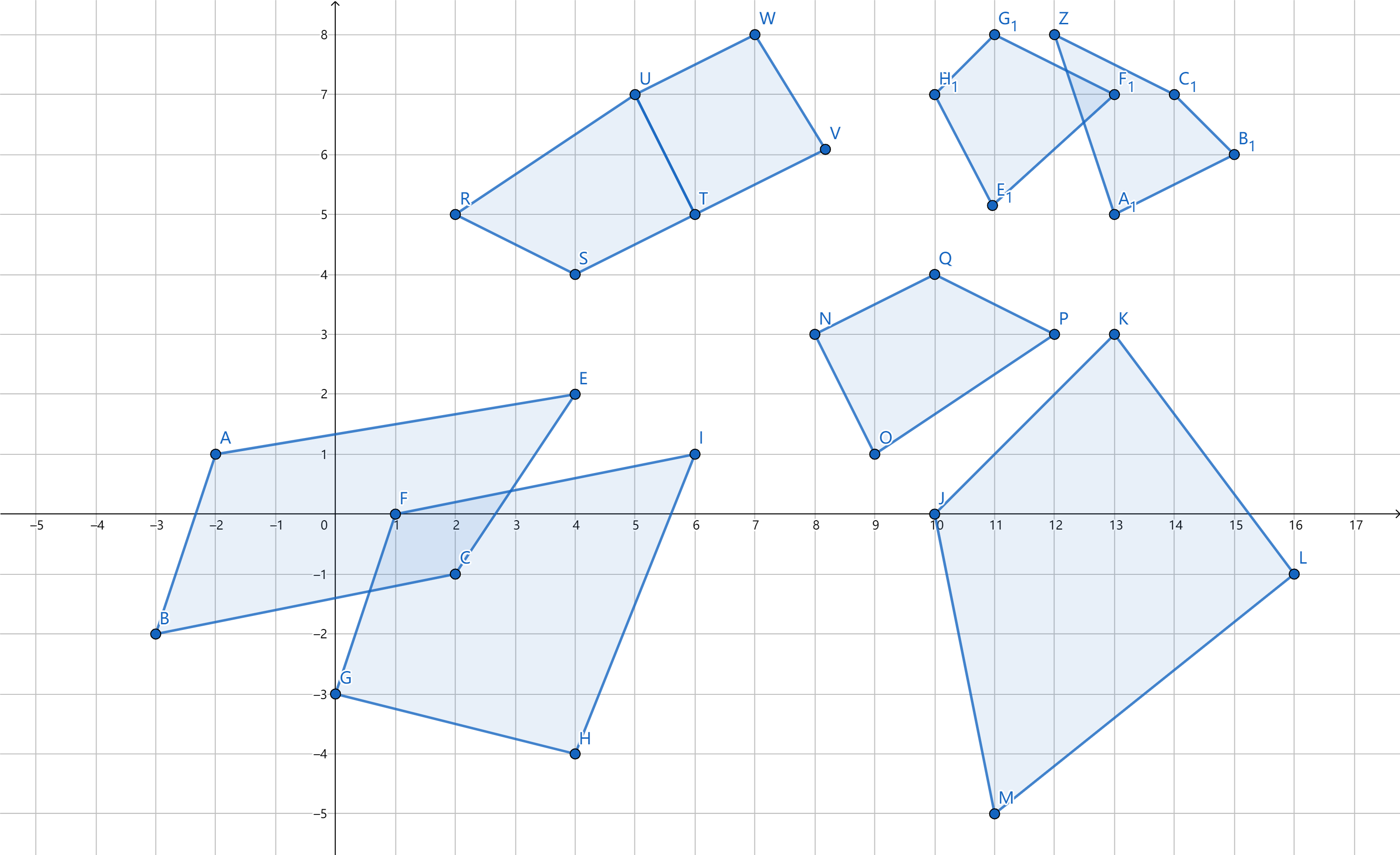
测试算法（上面的四边形）：

m_rectangle<int> r1 { {-2, 1},{-3, -2},{2, -1}, {4, 2} };
m_rectangle<int> r2 { {1, 0},{0, -3},{4, -4}, {6, 1} };
cout << m_check_intersect(r1, r2) << endl;

m_rectangle<int> r3{ {2, 5},{4, 4},{6, 5}, {5, 7} };
m_rectangle<int> r4{ {5, 7},{6, 5},{8, 6}, {7, 8} };
cout << m_check_intersect(r3, r4) << endl;

m_rectangle<int> r5{ {8, 3},{9, 1},{12, 3}, {10, 4} };
m_rectangle<int> r6{ {10, 0},{11, -5},{16, -1}, {13, 3} };
cout << m_check_intersect(r5, r6) << endl;

m_rectangle<int> r7{ {10, 7},{11, 5},{13, 7}, {11, 8} };
m_rectangle<int> r8{ {12, 8},{13, 5},{15, 6}, {14, 7} };
cout << m_check_intersect(r7, r8) << endl;

输出：

1
1
0
1

实现算法的代码如下：

template <typename T>
struct m_vector3D
{
	T x{ T() };
	T y{ T() };
	T z{ T() };
	m_vector3D (T _x, T _y, T _z):x(_x),y(_y),z(_z){}
	static m_vector3D m_dot_product(const m_vector3D& A, const m_vector3D& B)
	{
		return m_vector3D(A.x * B.x, A.y * B.y, A.z * B.z);
	}
	static m_vector3D m_cross_product(const m_vector3D& A, const m_vector3D& B) 
	{
		return m_vector3D(A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x);
	};
	m_vector3D operator+(const m_vector3D& rhs)
	{
		return m_vector3D(x + rhs.x, y + rhs.y, z + rhs.z);
	}
	m_vector3D operator-(const m_vector3D& rhs)
	{
		return m_vector3D(x - rhs.x, y - rhs.y, z - rhs.z);
	}
	m_vector3D operator*(const m_vector3D& rhs)
	{
		return m_vector3D(y * rhs.z - z * rhs.y, z * rhs.x - x * rhs.z, x * rhs.y - y * rhs.x);
	}
};

template <typename T>
struct m_rectangle
{
	struct m_point_2D
	{
		T x{ T() };
		T y{ T() };
		m_point_2D(){}
		m_point_2D(T _x, T _y) :x(_x), y(_y) {}
	};
	m_point_2D vertices[4];
	m_rectangle(m_point_2D p1, m_point_2D p2, m_point_2D p3, m_point_2D p4)
	{  	
		vertices[0] = std::move(p1);
		vertices[1] = std::move(p2);
		vertices[2] = std::move(p3);
		vertices[3] = std::move(p4);
	}
};

template <typename T>
bool m_check_intersect(const m_rectangle<T>& A, const m_rectangle<T>& B)
{
	// return the value z of AB × AP
	auto _AB_CROSS_AP = [](int ai, int bi, int pi, const m_rectangle<T>& M, const m_rectangle<T>& P)
	{
		m_vector3D<T> AB(M.vertices[bi].x - M.vertices[ai].x, M.vertices[bi].y - M.vertices[ai].y, static_cast<T>(0));
		m_vector3D<T> AP(P.vertices[pi].x - M.vertices[ai].x, P.vertices[pi].y - M.vertices[ai].y, static_cast<T>(0));
		return (AB * AP).z;
	};
	for (int i = 0; i < 4; ++i)
	{
		T v1 = _AB_CROSS_AP(0, 1, i, B, A);
		T v2 = _AB_CROSS_AP(1, 2, i, B, A);
		T v3 = _AB_CROSS_AP(2, 3, i, B, A);
		T v4 = _AB_CROSS_AP(3, 0, i, B, A);
		if (v1 == 0 || v2 == 0 || v3 == 0 || v4 == 0)
		{
			return true;
		}
		if (v1 * v2 > 0 && v1 * v3 > 0 && v1 * v4 > 0)
		{
			return true;
		}
	}
	for (int i = 0; i < 4; ++i)
	{
		T v1 = _AB_CROSS_AP(0, 1, i, A, B);
		T v2 = _AB_CROSS_AP(1, 2, i, A, B);
		T v3 = _AB_CROSS_AP(2, 3, i, A, B);
		T v4 = _AB_CROSS_AP(3, 0, i, A, B);
		if (v1 == 0 || v2 == 0 || v3 == 0 || v4 == 0)
		{
			return true;
		}
		if (v1 * v2 > 0 && v1 * v3 > 0 && v1 * v4 > 0)
		{
			return true;
		}
	}
	return false;
}